前面我们讲了费茨定律的理论内容,如果你认真消化后应该对费茨定律在研究什么,以及影响指点事件效率的关键因素已经有所了解了。(回顾:《费茨定律》)
为了让费茨定律更易于理解,今天我挑选了一些案例并加以总结,希望用真实的场景帮助你打开一些实操设计的思路。
前情提要:费茨定律指“指点动作消耗的时间T与距目标离D成正比,与目标大小W成反比。
一、费茨定律的常规思路
① 从距离切入的常规使用
1.1 对于起始点明确的指点事件
以前我在UI控件专题中分析导航栏使用方法的时候,有引用过滴滴的案例,谈到了我对滴滴的“取消订单”操作交互设计的看法,当时是将该操作与使用常规导航栏取消订单进行了对比。
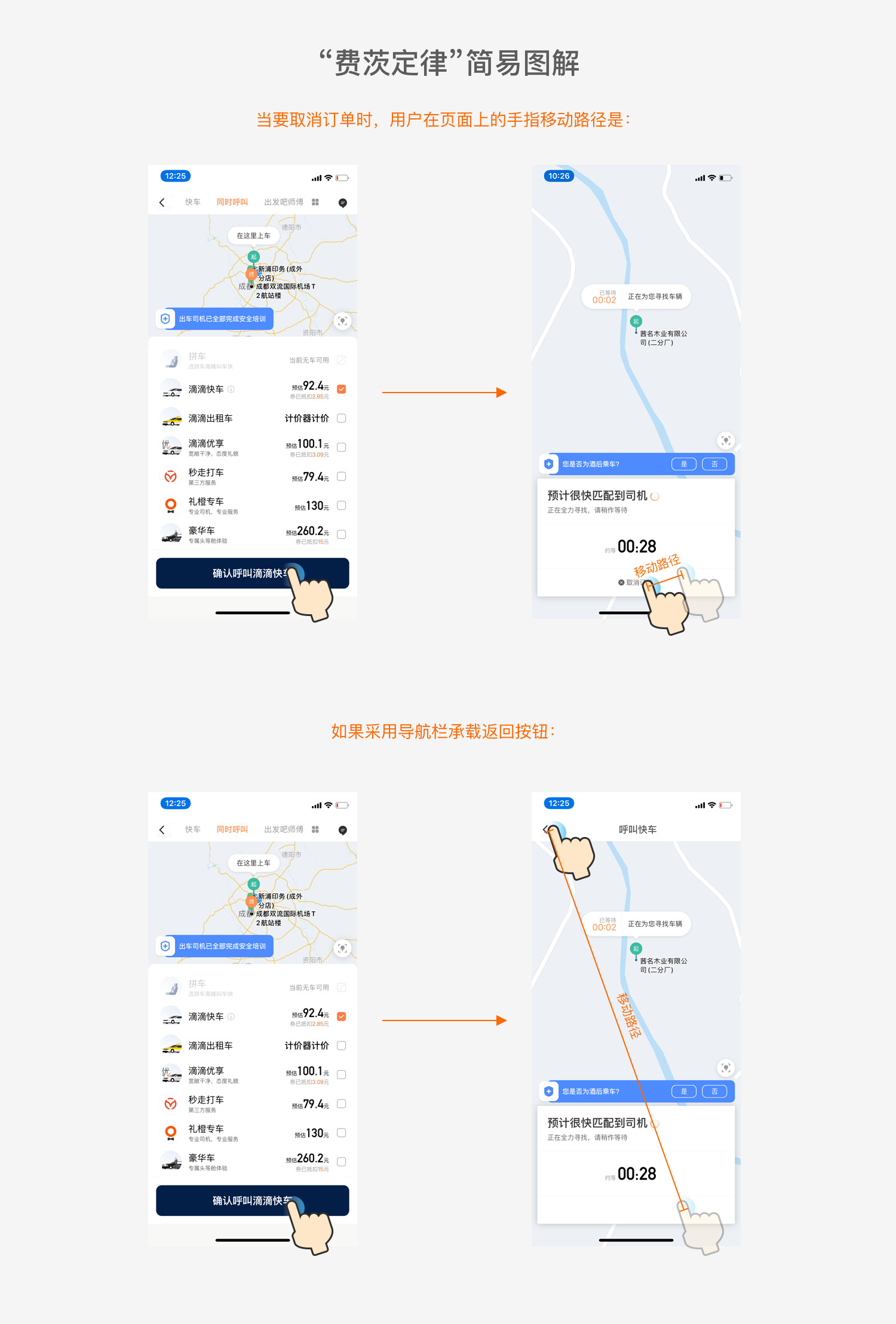
首先毋庸置疑,「取消订单」对于业务方来说是一项负向情绪操作(即:与业务流程、商业目标相悖的操作)。我们在日常设计界面与交互时,总是希望避免用户产生负向情绪操作,这一点对于久经沙场,常与产品、运营甚至老板对接的设计师朋友,应该能够达成共识。
所以我们看到滴滴对于「取消订单」操作采用了费茨定律中的减小目标区域大小W的设计,将「取消订单」按钮设计得小而不显眼。
但尽管我们总是在极力避免用户负向情绪操作,可也无法彻底规避特殊场景的产生。例如示例中,滴滴虽不希望用户取消订单,但依然无法规避用户误操作呼叫、等待时间过长等场景而导致需要取消订单的行为。
从上图中很容易看到,当用户点击「确认呼叫」时,点击「确认呼叫」按钮是一个起始点明确的指点事件,与「取消订单」的间距很小。对于有明确取消订单意愿的用户,可以快速方便地进行取消呼叫操作。
再例如PC端中,我们在任意位置点鼠标右键,都会在当前位置弹出右键菜单。点击鼠标的位置是明确的起始点,在就近位置弹出菜单可以大大降低目标与起始位置的距离。
主流移动端规范中,iOS与Material Design的气泡弹窗菜单,也和PC端右键菜单的设计有异曲同工之妙,在许多APP中也屡见不鲜。
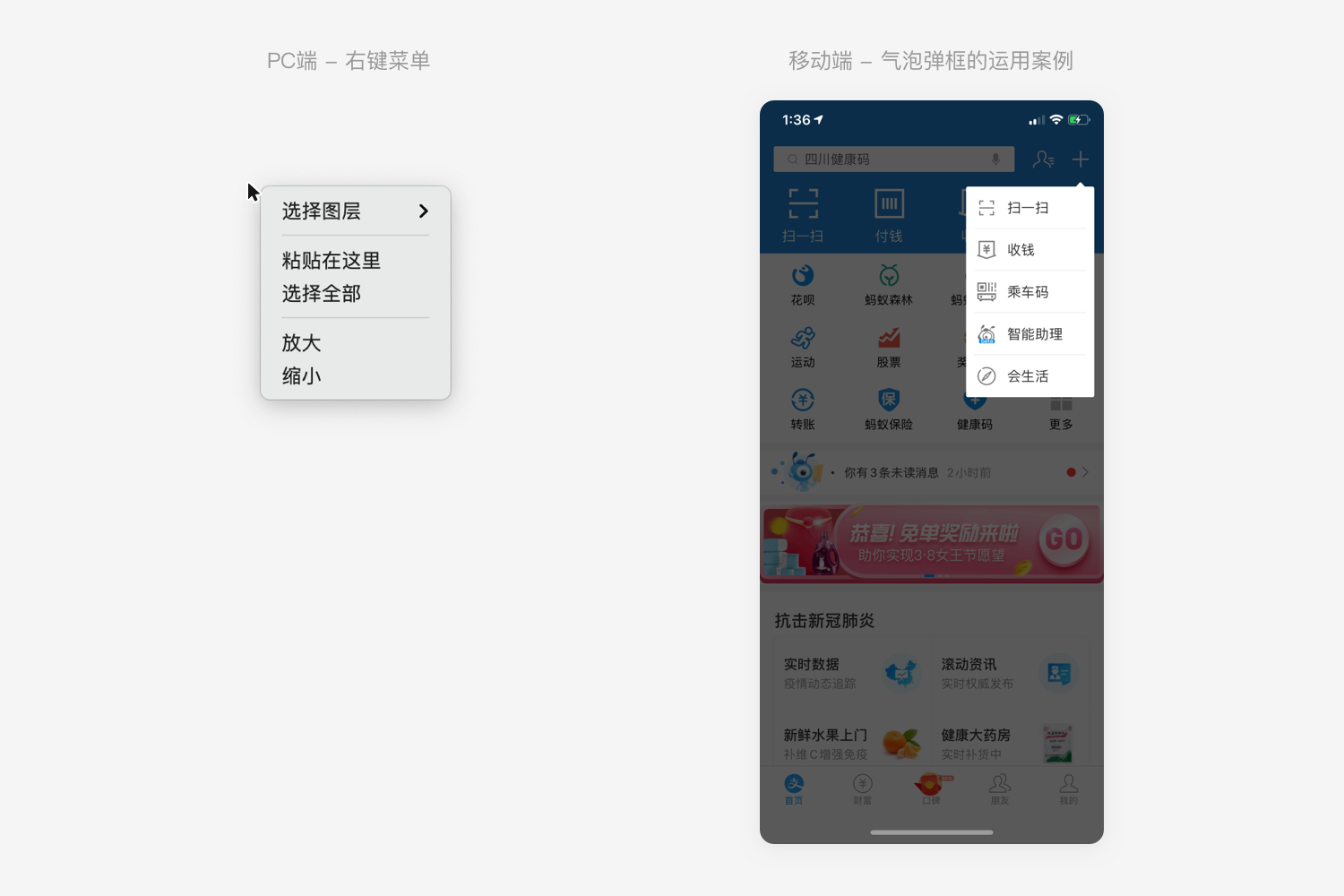
1.2 满足操作习惯的指点事件
有联动关系的功能场景其实是非常具体的,具体的案例当然比较少见,而抽象的场景其实才占据了我们设计需求中的绝大多数。有时候一个页面的功能繁多,我们无法具体弄清楚用户到底想要做什么。
举个例子,当用户点开一个电商历史订单,他想要做什么呢?查看物流、查看订单号、评价、复购、联系售后?可选择性太多。我们无法确定用户究竟想干嘛。
那我们来看看天猫是怎么做的:
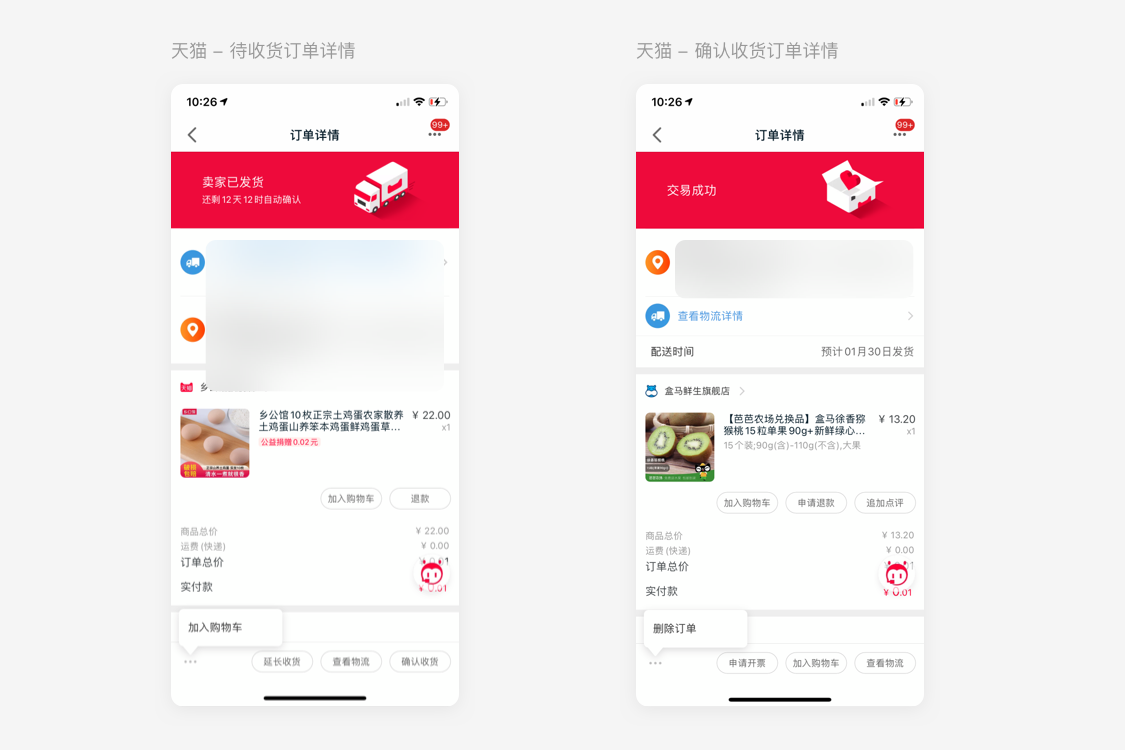
页面中的信息与功能非常多,且不同的订单状态设计到的功能展示也各不相同。但滑动页面时,始终有几个关键操作被固定在页面底部,并且居右排列。
和前面起始点明确的操作相比,我们的设计需求可能包含太多不能完全明确起始点的指点事件,但为了帮助用户做出选择,我们可以尽量使关键指点动作符合当前设备的操作习惯。
例如手机这样的小屏设备,我们拇指最常操作的区域就是屏幕的右侧中下部,拇指时常是停留在这个操作区域的,所以将主要功能操作放置在设备中下部,虽然不能明确起始点,但可以尽可能减小操作的移动距离。
帮助用户梳理繁多功能点中的功能优先级和操作频次数据,优先级高、频次高的操作可以结合当前操作设备的操作习惯,协助提高用户操作效率。
例如:当设计车载HMI时,我们是否可以考虑将司机高频功能,如广播、导航等置于偏主驾驶座方,方便司机操作;而次要功能可以放置于偏副驾驶座方。
② 从尺寸切入的常规使用
2.1 简单粗暴地放大按钮尺寸
对于功能点比较单一、页面内容比较简单的页面,放大按钮的尺寸一方面能够填充页面内容,同时也可以利于用户点击。
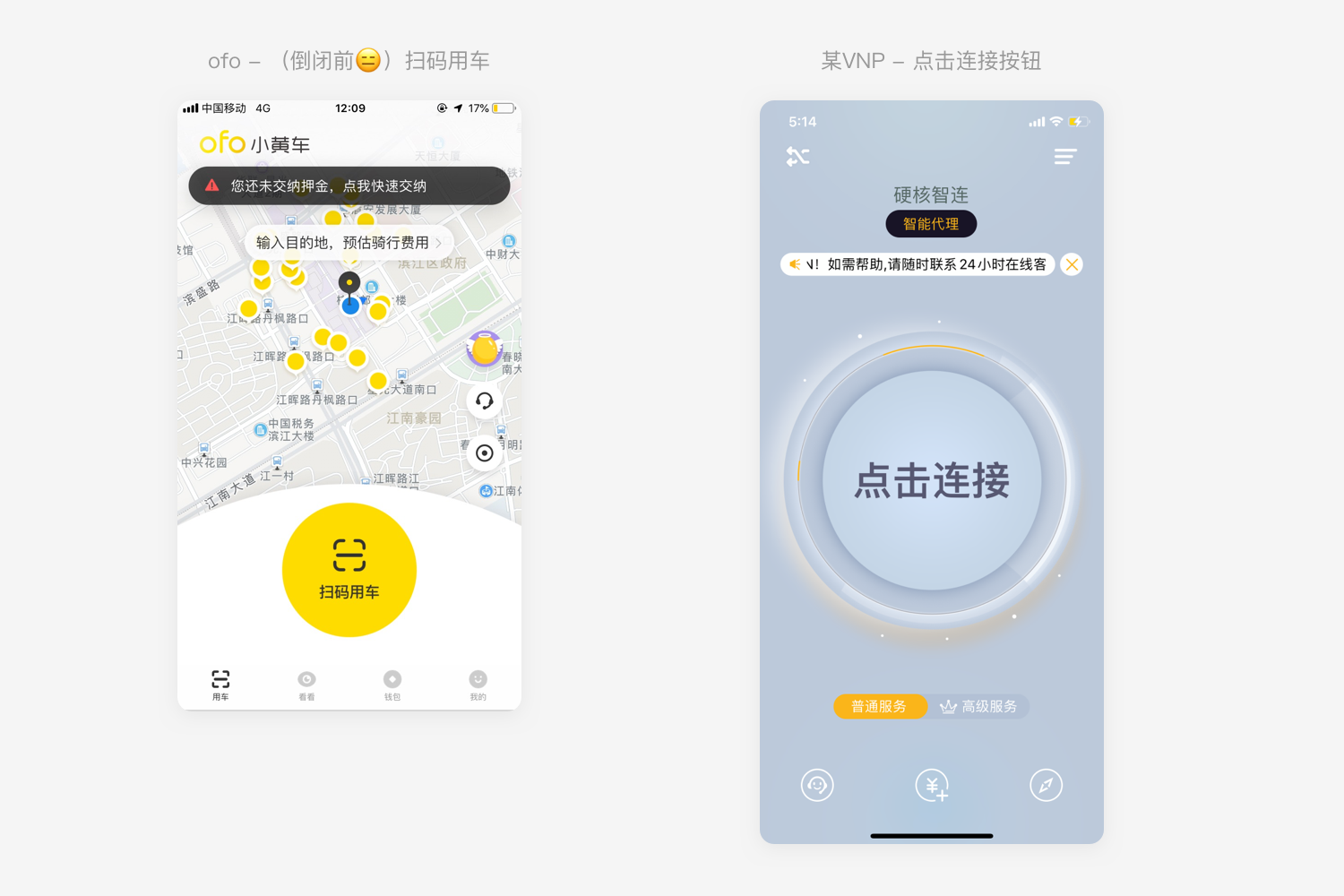
2.2 扩大操作热区
考虑到平衡视觉关系,我们可能无法为了提高用户操作体验,而在页面中将每一个操作都简单粗暴地放大。但我们可以选择在元素视觉大小不变的情况下,扩大触发操作的范围,即扩大热区。

我们可以根据页面具体内容排版,往两个方向思考:①直接扩大视觉元素;②保持视觉元素不变,扩大响应热区。两个方案分别是从UI和前端落地上切入,所以要记得有效沟通。
二、费茨定律的反向使用
以上我们所讲到的案例,都是通过正向思考产生的。但许多交互与UI设计中,反向思考、逆向使用费茨定律的例子,也不在少数。
这很好理解,当我们不希望让用户过于方便地操作的时候,我们就可以开始进行逆向思维,反向使用费茨定律,增加用户的操作难度。什么时候我们不希望用户过于方便地操作呢?——重要或危险操作需要用户小心谨慎,或者压根想阻挠用户操作的时候。
反向使用费茨定律最常被人引用的案例就是iOS的关机操作。
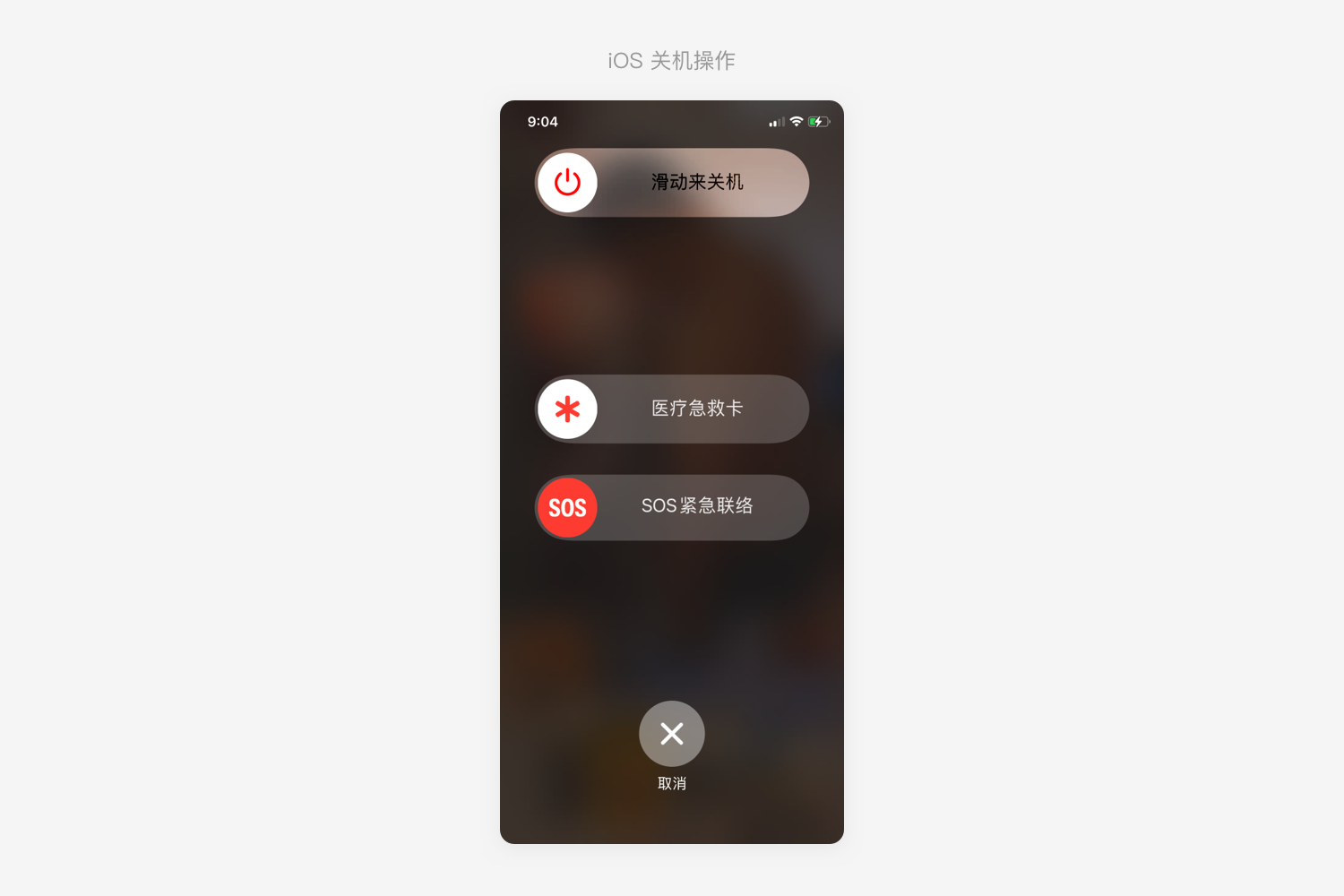
iOS的确认关机操作居于设备的顶部区域,是不太满足用户对手机的操作习惯的。其次通过滑动关机操作也增加了费茨定律中的「距离D」。各种反向设计都是为了提高用户操作的不便性,放置用户误操作。
同时费茨定律的反向使用方法在一些商业需求中也经常被使用。
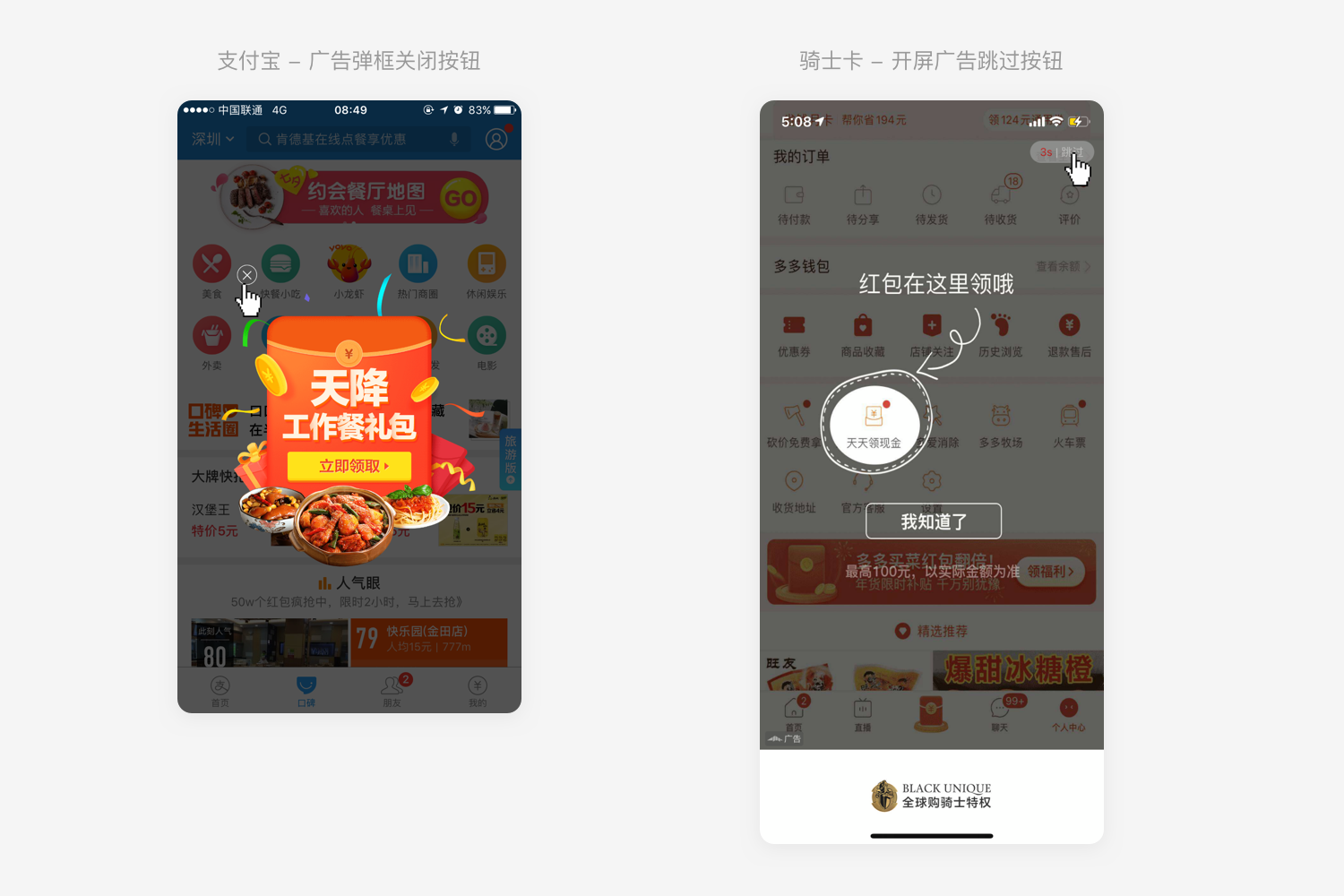
我们常常看到许多商业广告的关闭按钮被设计得很小,且点击区域也和用户习惯相悖,这也是反向使用费茨定律的案例。虽然从用户体验上来说,我们都希望尽量避免这些设计存在,但在商业价值面前,你懂的。
三、写在最后
最后我想再回到费茨定律的公式 T=a+blog2(D/W+1) 谈一谈对于设计法则的看法。
对高中数学还有一些记忆的朋友,应该对log函数不陌生,是求幂的逆运算。log函数往往会大幅抵消真数变化对底数的影响。我举个具体数值的例子:
我们如果简单记为T=log2(D/W),假设「距离D」是「大小W」的32倍,那么T=log2(32)=5。如果保持「大小W」不变,「距离D」缩小为原来的1/4,即「距离D」是「大小W」的8倍,那么T=log2(8)=3。
看到了吗,「距离D」虽然缩小了4倍,但因为log函数的影响,T缩小的倍数还不到原来的1/2。何况我们在移动设备交互设计中,时间T往往连一个整数秒都达不到,通常是毫秒级的,所以就算「距离D」与「大小W」比率成倍变化,对时间T最后的真实数值改变其实非常微小。
在对费茨定律的讲解结束之际,我讲这个是为了说明了什么呢?
我相信读者中,抱有“其实这样做和那样做,最后的实质性差别并不大嘛”想法的大有人在,但对于老前辈们写进书里的理论又羞于反驳。起初我时常和你们一样。
但随着做设计的时长越长,慢慢发现,多看多学“法则”其实往往是在巩固一种思维模式和思考方向,而这些我们装在脑中的东西往往比法则本身更有价值。对于费茨定律我希望大家不要像我起初抱着绝对的数学思想去理解,不然会走进一个胡同。多用开放思维去理解,可能更容易打开你设计的思想和对设计的理解~
原文地址:UCD耍家(公众号)
作者:Howiet









评论0